Day 7

Today

For next time

Survey Takeaways

Survey Debrief

  1. Your honest answers help us keep your workload in the sweetspot, where we are not burying you or boring you. Takewaway: For the most part, we hit the challenge sweet spot (we managed to avoid presenting too little challenge or too much challenge to most).

  2. We collect information about the structure of the MP and RJs - and consider them for how we scaffold future versions of the same assignment next semester (and when appropriate we use our learnings as we release subsequent RJs and MPs).

  3. We learn how people are utilizing the help structures, such as NINJAs. Takeaway: we confirmed that NINJA hours are being utilized well.

  4. This is a class where students can drive at their own desired speed, we see people who had familiarity with the programming concepts in MP1 challenging themselves. We learned how and why people are challenging themselves (e.g., trying out recursion just to see what would happen).

  5. There is no one-size fits all with how much structure we use as a starting scaffold, but we did pretty well in MP1

Reading Journal Debrief

First, with two other people sitting next to you, make sure you clarify any problems you ran into on the reading journal.

Next, with your same group, read through some sample solutions to the is_palindrome and is_power functions. For each solution answer the following questions.

  1. Is it correct?
  2. How readable is it? Note any changes that you think would improve the readability of the solution.

From Three Questions About Each Bug You Find:

  1. Is this mistake somewhere else also?
  2. What next bug is hidden behind this one?
  3. What should I do to prevent bugs like this?

What do you think about the effectiveness of these three questions? What questions do you ask yourself when debugging?

Recursion Practice

Pascal’s Triangle

Write a function called choose that takes two integer, n and k, and returns the number of ways to choose k items from a set of n (this is also known as the number of combinations of k items from a pool of n). Your solution should be implemented recursively using Pascal’s rule.

Levenshtein Distance

Write a function called levenshtein_distance that takes as input two strings and returns the Levenshtein distance between the two strings. Intuitively, the Levenshtein distance is the minimum number of edit operations to transform one string into the other (for this reason Levenshtein distance is sometimes called “edit distance”). These edits can either be insertions, deletions, or substitutions. Note that Levenshtein distance is similar to Hamming distance, but works for strings of differing lengths

Here are some examples of these operations:

  1. kitten → sitten (substitution of s for k)
  2. sitten → sittin (substitution of i for e)
  3. sittin → sitting (insertion of g at the end).

While this function seems initially daunting, it admits a very compact recursive solution. You can either work on your own to see the recursive solution, or use the recursive solution given in the Wikipedia article.

We will be memoizing this function in the next reading journal to make it more computationally efficient.

Making change

Write a program that takes as input a number of cents, n, along with the denominations of some coins, d, and outputs the number of unique ways that change can be made for n cents using the coins d.

For example:

make_change(10, [1, 5, 10])  # -> 4

Specifically:

Turtle World

Today we will be combining our adventures with turtles with our adventures with recursion. The results will astound you!

Teleportation, Cloning, and Other Unethical Experiments on Turtles

In addition to the what you did on your day 5 reading journal and in the day 6 class activity, a few other Turtle Tricks that may prove useful.

A Turtle is a Python object, which we will learn more about next week. Turtles have methods, which we can call to inspect change their behavior. One trick that will be useful here, which you saw in shapes.py but may not have thought about much, is the speed() function. The speed() function can be used to speed up slowpoke Turtles. While it seems weird that a speedy turtle would have a speed of 0, in this case the input 0 is reserved for having the turtle go as fast as possible (remember, when in doubt, check the documentation).

import turtle
speedy = turtle.Turtle()
speedy.speed(0)

Other important Turtle methods include xcor() and ycor() position, and heading().

Read more about turtles here.

Since Turtles are simple creatures, mainly defined by their current position and heading, we can “clone” them by reading these values and using them to direct a new Turtle.

leo = turtle.Turtle()
# leo does some arbitrary drawing (e.g., makes a 45 degree angle)
leo.fd(100)
leo.lt(45)
leo.fd(100)

# Create a new Turtle with the same attributes as the first
don = turtle.Turtle()
don.penup()
don.setx(leo.xcor())
don.sety(leo.ycor())
don.setheading(leo.heading())
if leo.isdown():
    don.pendown()
# don.bandana_color = "purple" # TODO: Ninja functionality not yet implemented

As an exercise, encapsulate this functionality in a clone function that takes a Turtle argument and returns a new Turtle with the same position and heading, leaving the original Turtle untouched.

Fractals

Fractals are geometrical constructions that display self-similar repeated patterns at every scale as you zoom in. They are often extremely beautiful, and are found throughout nature. Fractals are also useful across many fields, from antenna engineering to poetry to finance. Check out Yale’s Panorama of Fractals and their Uses for more examples.

Today, we will teach our turtles to draw fractal shapes using recursion. A very cool recursive drawing we can create is called the snowflake curve (or Koch snowflake). To get started, let’s write a function called snow_flake_side with the following signature:

def snow_flake_side(turtle, length, level):
    """Draw a side of the snowflake curve with side length length and recursion
    depth of level"""

The snow_flake_side function should have a base case that draws the following image:

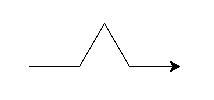
The recursive step should replace each of the line segments above with a snow_flake_side with size length / 3.0 and recursion depth level - 1. Take some time to work on this and then we’ll discuss as a group.

Once you have completed your snow_flake_side function, create a function called snow_flake that draws the whole snowflake.

Recursive Trees

Next, we will draw a tree using recursion. Define a function called recursive_tree that takes as input a turtle, a branch length, and a recursion depth and draws the recursive tree to the canvas.

def recursive_tree(turtle, branch_length, level):
    """Draw a tree with branch length branch_length and recursion depth of level
    """

The base case is:

This structure is given by moving forward branch_length steps (assuming the turtle has the correct orientation).

For the recursive step, you should:

  1. Draw the line as above
  2. Clone your turtle
  3. Turn the new turtle left 30 degrees
  4. Recurse using the cloned turtle to draw a tree with branch length branch_length * 0.6 and depth `level - 1
  5. Hide the cloned turtle using the hideturtle method
  6. Back the original turtle up branch_length / 3.0
  7. Clone your turtle
  8. Turn the new turtle right 40 degrees
  9. Recurse using the cloned turtle to draw a tree with branch length branch_length * 0.64 and depth level - 1
  10. Hide the cloned turtle using the hideturtle method

After implementing the recursive step, if you set level to 1 more than the base case (which will either be 1 or 2 depending on what level you consider the base case), you will get the following picture:

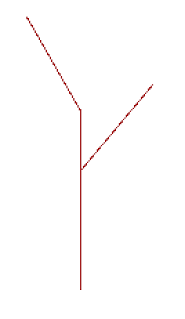
Once you’ve built your recursive_tree function, try making a few enhancements:

More Recursion

The Koch snowflake and our recursive tree are both part of a more general class of curves called L-systems (Lindenmayer Systems). Next, read the linked Wikipedia article on L-systems and try to implement Sierpinski’s triangle and fractal plant.

Hint 1: For Sierpinski’s triangle you will want to create a function to generate both symbols A and B and have them call each other.

Hint 2: For the fractal plant you should create the following functions to save and then restore then Turtle’s state (symbols [ and ] respectively):

def save_turtle_state(turtle_states, t):
    turtle_states.append((t.xcor(), t.ycor(), t.heading()))

def restore_turtle_state(turtle_states, t):
    s = turtle_states.pop()
    t.penup()
    t.setx(s[0])
    t.sety(s[1])
    t.setheading(s[2])
    t.pendown()